ACTF 2025
ACTF 2025 reverse engineering challenges
ezFPGA
Software is too slow… and hardware is too honest.
Dump cypher from .vcd file:
1
2
3
4
// Valid cypher values between 5500ns and 5860ns
uint8_t cypher_values[36] = {
0xAD, 0x00, 0xC0, 0x9F, 0x16, 0x17, 0xEC, 0x25, 0x25, 0x1F, 0x12, 0xE2, 0x7F, 0x9F, 0x37, 0x53, 0x12, 0xBA, 0x8D, 0x38, 0x60, 0x14, 0x1B, 0x31, 0x8E, 0x13, 0xE2, 0x56, 0x0A, 0x1A, 0x25, 0xB9, 0x80, 0x73, 0x8A, 0x60
};
Write a script to decrypt.
Event-Based: VCD doesn’t record the value of every signal at every tiny time step. Instead, it only records an entry when a signal’s value actually changes. This is more efficient than logging everything constantly.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
import numpy as np
from sympy import Matrix, gcd
from z3 import *
"""
Step 1: RC4
"""
def rc4(key: bytes, l) -> bytes:
# Key Scheduling Algorithm (KSA)
S = list(range(256))
j = 0
for i in range(256):
j = (j + S[i] + key[i % len(key)]) % 256
S[i], S[j] = S[j], S[i]
# Pseudo-Random Generation Algorithm (PRGA)
i = 0
j = 0
result = []
for _ in range(l):
i = (i + 1) % 256
j = (j + S[i]) % 256
S[i], S[j] = S[j], S[i]
k = S[(S[i] + S[j]) % 256]
result.append(k)
return bytes(result)
cypher_values = [
0xAD, 0x00, 0xC0, 0x9F, 0x16, 0x17, 0xEC, 0x25, 0x25, 0x1F,
0x12, 0xE2, 0x7F, 0x9F, 0x37, 0x53, 0x12, 0xBA, 0x8D, 0x38,
0x60, 0x14, 0x1B, 0x31, 0x8E, 0x13, 0xE2, 0x56, 0x0A, 0x1A,
0x25, 0xB9, 0x80, 0x73, 0x8A, 0x60
]
key = bytes([ord(c) for c in "eclipsky"])
keystream = rc4(key, len(cypher_values))
ae = [(c - k) % 256 for c, k in zip(cypher_values, keystream)]
"""
# Step 2: Invert AD matrix modulo 256
"""
ad_columns = [
[116, 11, 98, 31, 235, 15],
[174, 193, 214, 30, 25, 191],
[193, 115, 197, 117, 244, 119],
[124, 4, 145, 15, 202, 140],
[102, 127, 97, 230, 73, 94],
[100, 139, 151, 179, 222, 32]
]
ad_matrix = np.array(ad_columns).T.tolist()
sympy_matrix = Matrix(ad_matrix)
det = sympy_matrix.det() % 256
if gcd(det, 256) != 1:
raise ValueError("Matrix not invertible modulo 256")
inv_det = pow(int(det), -1, 256)
inv_matrix = (sympy_matrix.adjugate() * inv_det) % 256
inv_np = np.array(inv_matrix.tolist(), dtype=int) % 256
# Compute AC = AE * inv(AD) mod 256
ae_2d = np.array(ae).reshape(6, 6)
ac_2d = np.dot(ae_2d, inv_np) % 256
ac = ac_2d.flatten().tolist()
"""
Step 3: Set up Z3 solver with variable flag length constraints
"""
s = Solver()
aa = [BitVec(f'aa_{i}', 8) for i in range(39)]
# Fix the prefix "ACTF{"
prefix = [ord(c) for c in "ACTF{"]
for i in range(5):
s.add(aa[i] == prefix[i])
# Enforce flag ends with '}' and is followed by zeros
s.add(Or([aa[i] == ord('}') for i in range(5, 39)])) # At least one '}'
s.add(Sum([If(aa[i] == ord('}'), 1, 0) for i in range(5, 39)]) == 1) # Exactly one '}'
# Convolution equations for AC (36 equations)
for i in range(36):
term = (11 * aa[i] + 4 * aa[i + 1] + 5 * aa[i + 2] + 14 * aa[i + 3]) % 256
s.add(ac[i] == term)
if s.check() == sat:
model = s.model()
flag_bytes = [model[aa[i]].as_long() for i in range(39)]
print(bytes(flag_bytes))
else:
print("No solution found")
# ACTF{RC4_4nd_FPGA_w4lk_1nt0_4_b4r}
Deepx
Simply reversing PTX assembly - basic, but annoying. Solving these large loops requires either OpenMP or CUDA.
Also, some little problems were encountered.
Analysis of Layer1
1
2
3
4
5
6
7
8
9
10
float accumulated_value = 0.0f;
if (tid < 241 && bid < 241) {
for (unsigned int i = 0; i < 16; ++i) {
unsigned int index = (i + bid) * bdm + tid;
unsigned int motion_row = 240 - (i * 16);
for (unsigned int j = 0; j < 16; ++j) {
accumulated_value += MOTION[motion_row + j] * (float)input[index + j]
}
}
}
Analysis of Layer2
1
2
3
4
5
6
unsigned int bid = %ctaid.x;
unsigned int tid = %tid.x;
unsigned int bdm= %ntid.x;
int i = bdm * bid + tid;
output[ bdm * SBOX[tid]+ SBOX[bid] ] = input[i];
// output[SBOX[tid], SBOX[bid]] = input[bid, tid]
It’s a mapping of each coordinate. The process is as follows:
- Forward mapping:
swap→apply SBOX - Inverse mapping:
apply INV_SBOX→swap
Analysis of Layer3
Part 1: XOR + TEA + XOR
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// XOR step
const uint32_t tid = threadIdx.x; // Thread index within block (0-255)
const uint32_t bid = blockIdx.x; // Block index within grid (0-255)
input[i] ^= bid | tid
bar.sync
// TEA step
const uint32_t K0 = 1386807340;
const uint32_t K1 = 2007053320;
const uint32_t K2 = 621668851;
const uint32_t K3 = -862448841
const uint32_t DELTA = -1708609273
uint32_t sum = 1786956040; // Initial sum
for (uint32_t i = 0; i < 3238567; ++i) {
uint32_t term1 = (data0 << 4) + K0;
uint32_t term2 = (data0 >> 5) + K1; // logical right shift
uint32_t term3 = data0 + sum;
data1 += (term1 ^ term2) ^ term3; // Update data1
uint32_t term4 = (data1 << 4) + K2;
uint32_t term5 = sum + data1;
uint32_t term6 = (data1 >> 5) + K3; // logical right shift
data0 -= (term4 ^ term5) ^ term6; // Update data0
sum += DELTA;
}
bar.sync
// XOR step
input[i] ^= bid & tid
bar.sync
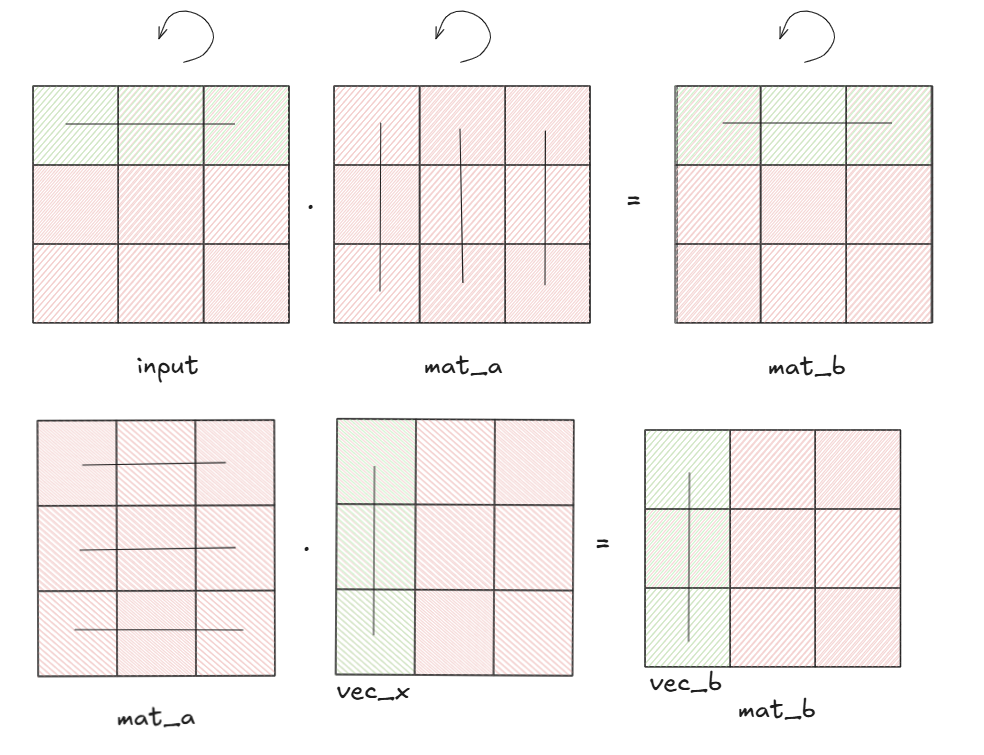
Part 2: Matrix multiplication
\[input \cdot mat_a = mat_b\]1
2
3
4
5
6
7
8
uint8_t input[256 * 256];
uint8_t result = 0;
uint8_t *base = input + bid * 256;
uint8_t sum = SBOX[tid];
for (uint32_t i = 0; i < 256; ++i) {
result += base[i] * TBOX[sum];
sum = sum * 5 + 17;
}
Part 3: ROL + LCG + XOR + SBOX
1
2
3
4
5
6
7
8
9
10
11
12
13
// Layer_3_part_3
input[256 * 256];
uint8_t i = bid * 256 + tid;
uint8_t key = bid ^ tid;
uint8_t result_3= input[i];
for (uint32_t j = 8; j < 4137823; ++j) {
uint8_t result_1 = (result_3 << 3) | (result_3>> 5); // rotate left 3
uint8_t result_2 = result_1 * 13 + key;
result_3 = cuda_sbox[cuda_tbox[j & 0xFF] ^ result_2];
}
output[i] = result_3;
Decrypt Script
L3 - Part 3: ROL + LCG + XOR + SBOX
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
// part_3.cpp
#include <cstdint>
#include <vector>
#include <fstream>
#include <omp.h>
#include <iostream>
#include <cassert>
#define DEBUG
uint8_t SBOX[256] = { ... };
uint8_t TBOX[256] = { ... };
uint8_t INVSBOX[256];
void compute_inv()
{
for (int i = 0; i < 256; i++)
INVSBOX[SBOX[i]] = i;
}
static uint8_t kernel(int i, uint8_t b3)
{
uint8_t bid = i / 256;
uint8_t tid = i % 256;
uint8_t key = bid ^ tid;
uint8_t b1, b2;
for (int j = 4137822; j >= 8; j--)
{
b2 = INVSBOX[b3] ^ TBOX[j & 0xFF];
b1 = (b2 - key) * 197;
b3 = (b1 << 5) | (b1 >> 3); // rotate right 3
}
return b3;
}
int main()
{
compute_inv();
std::ifstream in_file("deep_flag.bin", std::ios::binary);
#ifdef DEBUG
assert(in_file.is_open());
#endif
in_file.seekg(0, std::ios::end);
size_t file_size = in_file.tellg();
#ifdef DEBUG
assert(file_size == 256 * 256);
#endif
in_file.seekg(0, std::ios::beg);
std::vector<uint8_t> input_data(file_size);
in_file.read(reinterpret_cast<char *>(input_data.data()), file_size);
in_file.close();
const uint8_t *input = input_data.data();
std::vector<uint8_t> output(256 * 256);
#pragma omp parallel for schedule(static)
for (int i = 0; i < 256 * 256; ++i)
{
output[i] = kernel(i, input[i]);
}
std::ofstream out_file("part_3_in.bin", std::ios::binary);
out_file.write(reinterpret_cast<const char *>(output.data()), output.size());
out_file.close();
return 0;
}
// Usage: g++ .\part_3.cpp -o part_3.exe -fopenmp -std=c++17 -O2 -Wall
A little problem:
g++ .\part_3.cpp -o part_3.exe -fopenmp. The executable compiled with this command do not reach full CPU utilization of each logical processors. However,g++ .\part_3.cpp -o part_3.exe -fopenmp -std=c++17 -O2 -Wallutilize CPU to 100%. Why?Switching on
–O2 –std=c++17 –Wall(or any –O2/–O3), the compiler:• inlines
kernel(…)into the hot OpenMP loop• promotes
b1,b2,b3,j,keyinto registers• emits a single ROR instruction for the rotate
• hoists loads of the constant
SBOX/TBOX/INVSBOXinto contiguous register lookups• unrolls/strength-reduces the loop and generally cleans out all of the stack traffic
So, be aware of using compiler optimizations for better CPU utilization.
L3 - Part 2: Matrix Multiplication
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
# part_2.sage
import functools as ft
import tqdm
from sage.all import *
# fmt: off
SBOX = bytes([ ... ])
# SBOX_INV = bytes(SBOX.index(i) for i in range(256))
TBOX = bytes([ ... ])
# TBOX_INV = bytes((TBOX.index(i) for i in range(256)))
# fmt: on
THREADS_PER_BLOCK = 256
Zmod256 = Integers(256)
# @ft.cache
def get_coeff(thread_id: int):
s = SBOX[thread_id]
coeffs = []
for _ in range(THREADS_PER_BLOCK):
coeffs.append(TBOX[s & 0xFF])
s = ((s * 5) + 17) & 0xFF
return vector(Zmod256, coeffs)
# @ft.cache
def get_coeff_mat():
rows = []
for j in range(THREADS_PER_BLOCK):
rows.append(get_coeff(j))
return Matrix(Zmod256, rows)
with open("part_3_in.bin", "rb") as f:
in_buf = f.read()
assert len(in_buf) % THREADS_PER_BLOCK == 0
results = []
mat_a = get_coeff_mat()
for i in tqdm.tqdm(range(len(in_buf) // THREADS_PER_BLOCK)):
vec_b = vector(Zmod256, in_buf[i * THREADS_PER_BLOCK : (i + 1) * THREADS_PER_BLOCK])
vec_x = mat_a.solve_right(vec_b)
results.extend(vec_x)
with open("part_2_in.bin", "wb") as f:
f.write(bytes(results))
Let’s try to get a more intuitive understanding of this solution process, which is equivalent to solving $Ax = b$ 256 times, where $x$ is a 256-entry vector consisting each row of the original 256 * 256 input image:
1
2
3
4
for i in tqdm.tqdm(range(len(in_buf) // THREADS_PER_BLOCK)):
vec_b = vector(Zmod256, in_buf[i * THREADS_PER_BLOCK : (i + 1) * THREADS_PER_BLOCK])
vec_x = mat_a.solve_right(vec_b)
results.extend(vec_x)
L3 - Part 1: XOR + TEA + XOR
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
// part_1.cpp
#include <stdio.h>
#include <cstdint>
#include <vector>
#include <iostream>
#include <fstream>
#include <cassert>
#define DEBUG
const uint32_t K0 = 1386807340;
const uint32_t K1 = 2007053320;
const uint32_t K2 = 621668851;
const uint32_t K3 = -862448841;
void tea_kernel(uint32_t v[2]) {
uint32_t v0 = v[0], v1 = v[1], delta = -1708609273, sum = 1786956040 + delta * 3238567;
for (int i = 0; i < 3238567; i++) {
sum -= delta;
v0 += ((v1 << 4) + K2) ^ (v1 + sum) ^ ((v1 >> 5) + K3);
v1 -= ((v0 << 4) + K0) ^ (v0 + sum) ^ ((v0 >> 5) + K1);
}
v[0] = v0;
v[1] = v1;
}
int main(){
std::ifstream in_file("part_2_in.bin", std::ios::binary);
#ifdef DEBUG
assert(in_file.is_open());
#endif
in_file.seekg(0, std::ios::end);
size_t file_size = in_file.tellg();
in_file.seekg(0, std::ios::beg);
#ifdef DEBUG
assert(file_size == 256 * 256);
assert(in_file.tellg() == 0);
#endif
std::vector<uint8_t> input(file_size);
in_file.read(reinterpret_cast<char *>(input.data()), file_size);
in_file.close();
uint8_t *input_ptr = input.data();
// Granularity: BYTE
#pragma omp parallel for schedule(static)
for(size_t i = 0; i < file_size; i++){
uint8_t bid = i / 256;
uint8_t tid = i % 256;
input_ptr[i] ^= bid & tid;
}
// Granularity: QWORD
#pragma omp parallel for schedule(static)
for(size_t i = 0; i < file_size; i += 8){
tea_kernel((uint32_t *)&input_ptr[i]);
}
// Granularity: BYTE
#pragma omp parallel for schedule(static)
for(size_t i = 0; i < file_size; i++){
uint8_t bid = i / 256;
uint8_t tid = i % 256;
input_ptr[i] ^= bid | tid;
}
std::ofstream out_file("part_1_in.bin", std::ios::binary);
out_file.write(reinterpret_cast<char *>(input_ptr), file_size);
return 0;
}
L2 - Mapping
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# layer_2.py
import tqdm
SBOX = bytes([ ... ])
"""
input: value
output: index
"""
INV_SBOX = bytes([SBOX.index(i) for i in range(256)])
assert len(SBOX) == 256
BMP = bytes([0x42,0x4d,0x36,0x04,0x01,0x00,0x00,0x00,0x00,0x00,0x36,0x04,0x00,0x00,0x28,0x00,0x00,0x00,0x00,0x01,0x00,0x00,0x00,0x01,0x00,0x00,0x01,0x00,0x08,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x01,0x01,0x01,0x00,0x02,0x02,0x02,0x00,0x03,0x03,0x03,0x00,0x04,0x04,0x04,0x00,0x05,0x05,0x05,0x00,0x06,0x06,0x06,0x00,0x07,0x07,0x07,0x00,0x08,0x08,0x08,0x00,0x09,0x09,0x09,0x00,0x0a,0x0a,0x0a,0x00,0x0b,0x0b,0x0b,0x00,0x0c,0x0c,0x0c,0x00,0x0d,0x0d,0x0d,0x00,0x0e,0x0e,0x0e,0x00,0x0f,0x0f,0x0f,0x00,0x10,0x10,0x10,0x00,0x11,0x11,0x11,0x00,0x12,0x12,0x12,0x00,0x13,0x13,0x13,0x00,0x14,0x14,0x14,0x00,0x15,0x15,0x15,0x00,0x16,0x16,0x16,0x00,0x17,0x17,0x17,0x00,0x18,0x18,0x18,0x00,0x19,0x19,0x19,0x00,0x1a,0x1a,0x1a,0x00,0x1b,0x1b,0x1b,0x00,0x1c,0x1c,0x1c,0x00,0x1d,0x1d,0x1d,0x00,0x1e,0x1e,0x1e,0x00,0x1f,0x1f,0x1f,0x00,0x20,0x20,0x20,0x00,0x21,0x21,0x21,0x00,0x22,0x22,0x22,0x00,0x23,0x23,0x23,0x00,0x24,0x24,0x24,0x00,0x25,0x25,0x25,0x00,0x26,0x26,0x26,0x00,0x27,0x27,0x27,0x00,0x28,0x28,0x28,0x00,0x29,0x29,0x29,0x00,0x2a,0x2a,0x2a,0x00,0x2b,0x2b,0x2b,0x00,0x2c,0x2c,0x2c,0x00,0x2d,0x2d,0x2d,0x00,0x2e,0x2e,0x2e,0x00,0x2f,0x2f,0x2f,0x00,0x30,0x30,0x30,0x00,0x31,0x31,0x31,0x00,0x32,0x32,0x32,0x00,0x33,0x33,0x33,0x00,0x34,0x34,0x34,0x00,0x35,0x35,0x35,0x00,0x36,0x36,0x36,0x00,0x37,0x37,0x37,0x00,0x38,0x38,0x38,0x00,0x39,0x39,0x39,0x00,0x3a,0x3a,0x3a,0x00,0x3b,0x3b,0x3b,0x00,0x3c,0x3c,0x3c,0x00,0x3d,0x3d,0x3d,0x00,0x3e,0x3e,0x3e,0x00,0x3f,0x3f,0x3f,0x00,0x40,0x40,0x40,0x00,0x41,0x41,0x41,0x00,0x42,0x42,0x42,0x00,0x43,0x43,0x43,0x00,0x44,0x44,0x44,0x00,0x45,0x45,0x45,0x00,0x46,0x46,0x46,0x00,0x47,0x47,0x47,0x00,0x48,0x48,0x48,0x00,0x49,0x49,0x49,0x00,0x4a,0x4a,0x4a,0x00,0x4b,0x4b,0x4b,0x00,0x4c,0x4c,0x4c,0x00,0x4d,0x4d,0x4d,0x00,0x4e,0x4e,0x4e,0x00,0x4f,0x4f,0x4f,0x00,0x50,0x50,0x50,0x00,0x51,0x51,0x51,0x00,0x52,0x52,0x52,0x00,0x53,0x53,0x53,0x00,0x54,0x54,0x54,0x00,0x55,0x55,0x55,0x00,0x56,0x56,0x56,0x00,0x57,0x57,0x57,0x00,0x58,0x58,0x58,0x00,0x59,0x59,0x59,0x00,0x5a,0x5a,0x5a,0x00,0x5b,0x5b,0x5b,0x00,0x5c,0x5c,0x5c,0x00,0x5d,0x5d,0x5d,0x00,0x5e,0x5e,0x5e,0x00,0x5f,0x5f,0x5f,0x00,0x60,0x60,0x60,0x00,0x61,0x61,0x61,0x00,0x62,0x62,0x62,0x00,0x63,0x63,0x63,0x00,0x64,0x64,0x64,0x00,0x65,0x65,0x65,0x00,0x66,0x66,0x66,0x00,0x67,0x67,0x67,0x00,0x68,0x68,0x68,0x00,0x69,0x69,0x69,0x00,0x6a,0x6a,0x6a,0x00,0x6b,0x6b,0x6b,0x00,0x6c,0x6c,0x6c,0x00,0x6d,0x6d,0x6d,0x00,0x6e,0x6e,0x6e,0x00,0x6f,0x6f,0x6f,0x00,0x70,0x70,0x70,0x00,0x71,0x71,0x71,0x00,0x72,0x72,0x72,0x00,0x73,0x73,0x73,0x00,0x74,0x74,0x74,0x00,0x75,0x75,0x75,0x00,0x76,0x76,0x76,0x00,0x77,0x77,0x77,0x00,0x78,0x78,0x78,0x00,0x79,0x79,0x79,0x00,0x7a,0x7a,0x7a,0x00,0x7b,0x7b,0x7b,0x00,0x7c,0x7c,0x7c,0x00,0x7d,0x7d,0x7d,0x00,0x7e,0x7e,0x7e,0x00,0x7f,0x7f,0x7f,0x00,0x80,0x80,0x80,0x00,0x81,0x81,0x81,0x00,0x82,0x82,0x82,0x00,0x83,0x83,0x83,0x00,0x84,0x84,0x84,0x00,0x85,0x85,0x85,0x00,0x86,0x86,0x86,0x00,0x87,0x87,0x87,0x00,0x88,0x88,0x88,0x00,0x89,0x89,0x89,0x00,0x8a,0x8a,0x8a,0x00,0x8b,0x8b,0x8b,0x00,0x8c,0x8c,0x8c,0x00,0x8d,0x8d,0x8d,0x00,0x8e,0x8e,0x8e,0x00,0x8f,0x8f,0x8f,0x00,0x90,0x90,0x90,0x00,0x91,0x91,0x91,0x00,0x92,0x92,0x92,0x00,0x93,0x93,0x93,0x00,0x94,0x94,0x94,0x00,0x95,0x95,0x95,0x00,0x96,0x96,0x96,0x00,0x97,0x97,0x97,0x00,0x98,0x98,0x98,0x00,0x99,0x99,0x99,0x00,0x9a,0x9a,0x9a,0x00,0x9b,0x9b,0x9b,0x00,0x9c,0x9c,0x9c,0x00,0x9d,0x9d,0x9d,0x00,0x9e,0x9e,0x9e,0x00,0x9f,0x9f,0x9f,0x00,0xa0,0xa0,0xa0,0x00,0xa1,0xa1,0xa1,0x00,0xa2,0xa2,0xa2,0x00,0xa3,0xa3,0xa3,0x00,0xa4,0xa4,0xa4,0x00,0xa5,0xa5,0xa5,0x00,0xa6,0xa6,0xa6,0x00,0xa7,0xa7,0xa7,0x00,0xa8,0xa8,0xa8,0x00,0xa9,0xa9,0xa9,0x00,0xaa,0xaa,0xaa,0x00,0xab,0xab,0xab,0x00,0xac,0xac,0xac,0x00,0xad,0xad,0xad,0x00,0xae,0xae,0xae,0x00,0xaf,0xaf,0xaf,0x00,0xb0,0xb0,0xb0,0x00,0xb1,0xb1,0xb1,0x00,0xb2,0xb2,0xb2,0x00,0xb3,0xb3,0xb3,0x00,0xb4,0xb4,0xb4,0x00,0xb5,0xb5,0xb5,0x00,0xb6,0xb6,0xb6,0x00,0xb7,0xb7,0xb7,0x00,0xb8,0xb8,0xb8,0x00,0xb9,0xb9,0xb9,0x00,0xba,0xba,0xba,0x00,0xbb,0xbb,0xbb,0x00,0xbc,0xbc,0xbc,0x00,0xbd,0xbd,0xbd,0x00,0xbe,0xbe,0xbe,0x00,0xbf,0xbf,0xbf,0x00,0xc0,0xc0,0xc0,0x00,0xc1,0xc1,0xc1,0x00,0xc2,0xc2,0xc2,0x00,0xc3,0xc3,0xc3,0x00,0xc4,0xc4,0xc4,0x00,0xc5,0xc5,0xc5,0x00,0xc6,0xc6,0xc6,0x00,0xc7,0xc7,0xc7,0x00,0xc8,0xc8,0xc8,0x00,0xc9,0xc9,0xc9,0x00,0xca,0xca,0xca,0x00,0xcb,0xcb,0xcb,0x00,0xcc,0xcc,0xcc,0x00,0xcd,0xcd,0xcd,0x00,0xce,0xce,0xce,0x00,0xcf,0xcf,0xcf,0x00,0xd0,0xd0,0xd0,0x00,0xd1,0xd1,0xd1,0x00,0xd2,0xd2,0xd2,0x00,0xd3,0xd3,0xd3,0x00,0xd4,0xd4,0xd4,0x00,0xd5,0xd5,0xd5,0x00,0xd6,0xd6,0xd6,0x00,0xd7,0xd7,0xd7,0x00,0xd8,0xd8,0xd8,0x00,0xd9,0xd9,0xd9,0x00,0xda,0xda,0xda,0x00,0xdb,0xdb,0xdb,0x00,0xdc,0xdc,0xdc,0x00,0xdd,0xdd,0xdd,0x00,0xde,0xde,0xde,0x00,0xdf,0xdf,0xdf,0x00,0xe0,0xe0,0xe0,0x00,0xe1,0xe1,0xe1,0x00,0xe2,0xe2,0xe2,0x00,0xe3,0xe3,0xe3,0x00,0xe4,0xe4,0xe4,0x00,0xe5,0xe5,0xe5,0x00,0xe6,0xe6,0xe6,0x00,0xe7,0xe7,0xe7,0x00,0xe8,0xe8,0xe8,0x00,0xe9,0xe9,0xe9,0x00,0xea,0xea,0xea,0x00,0xeb,0xeb,0xeb,0x00,0xec,0xec,0xec,0x00,0xed,0xed,0xed,0x00,0xee,0xee,0xee,0x00,0xef,0xef,0xef,0x00,0xf0,0xf0,0xf0,0x00,0xf1,0xf1,0xf1,0x00,0xf2,0xf2,0xf2,0x00,0xf3,0xf3,0xf3,0x00,0xf4,0xf4,0xf4,0x00,0xf5,0xf5,0xf5,0x00,0xf6,0xf6,0xf6,0x00,0xf7,0xf7,0xf7,0x00,0xf8,0xf8,0xf8,0x00,0xf9,0xf9,0xf9,0x00,0xfa,0xfa,0xfa,0x00,0xfb,0xfb,0xfb,0x00,0xfc,0xfc,0xfc,0x00,0xfd,0xfd,0xfd,0x00,0xfe,0xfe,0xfe,0x00,0xff,0xff,0xff,0x00])
assert len(BMP) == 0x436
with open("part_1_in.bin", "rb") as in_file:
input = in_file.read()
assert len(input) == 256 * 256
output = bytearray(256 * 256)
bdm = 256
with open("layer_2_in.bmp", "wb") as f:
for i in tqdm.tqdm(range(256 * 256)):
tid = i % 256
bid = i // 256
output[INV_SBOX[tid] * bdm + INV_SBOX[bid]] = input[bid * bdm + tid] # Swap and apply INV_SBOX
f.write(BMP)
f.write(output)
Extract the convolutional kernel for motion blur:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
# format_IDA_data.py
import re
import struct
def parse_rodata_floats(data_string):
"""
Parses a string containing .rodata definitions and extracts float values.
Args:
data_string: A multiline string containing the .rodata dump.
Returns:
A list of floats extracted from the data.
"""
all_floats = []
lines = data_string.strip().split('\n')
for line_number, line in enumerate(lines, 1):
# Look for lines containing 'dd ' which signifies data definition
if 'dd ' not in line:
continue
try:
# Split by 'dd ' and take the second part
data_part = line.split(' dd ', 1)[1]
# Remove comments if any (stuff after ';')
if ';' in data_part:
data_part = data_part.split(';', 1)[0]
potential_floats = data_part.split(',')
for val_str in potential_floats:
cleaned_val_str = val_str.strip()
if cleaned_val_str:
try:
all_floats.append(float(cleaned_val_str))
except ValueError:
print(f"Warning (line {line_number}): Could not convert '{cleaned_val_str}' to float from: \"{line.strip()}\"")
except IndexError:
print(f"Warning (line {line_number}): Malformed line or unexpected structure after 'dd ': \"{line.strip()}\"")
continue
return all_floats
def save_floats_to_file(floats_list, output_filename):
"""
Saves a list of floats to a text file, one float per line.
Args:
floats_list: A list of float numbers.
output_filename: The name of the file to save the floats to.
Returns:
True if saving was successful, False otherwise.
"""
write_buf = []
with open(output_filename, 'w') as f:
for item in floats_list:
write_buf.append(str(item))
f.write(', '.join(write_buf))
print(f"Successfully saved {len(floats_list)} numbers to '{output_filename}'")
return True
# The data provided by the user
rodata_input = """
.rodata:0000000000483020 _ZL6motion dd 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.012483786, 0.042622309
...
.rodata:00000000004833E0 dd 0.0, 0.0055596731, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0
"""
if __name__ == "__main__":
# Parse the data
print("Parsing rodata input...")
extracted_floats = parse_rodata_floats(rodata_input)
if extracted_floats:
print(f"Successfully parsed {len(extracted_floats)} numbers.")
# Define the output filename
output_file = "extracted_data.txt"
# Save the floats to the text file
save_floats_to_file(extracted_floats, output_file)
else:
print("No floats were extracted from the input.")
Using Wiener algorithm to deconvolute:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import numpy as np
import matplotlib.pyplot as plt
from skimage import io, restoration
# Load and reshape PSF to 16x16
psf = np.array([ ... ])
kernel = psf.reshape(16, 16)
assert(len(psf) == 256)
print(psf.sum())
psf = psf.reshape((16, 16))
# Load image as grayscale
image = io.imread('layer_2_in.bmp', as_gray=True)[15:255, 0:240]
print(len(image))
# Perform deconvolution
deconvolved = restoration.wiener(
image=image,
psf=psf,
balance = 0.00001,
clip=False
)
# Visualization (unchanged)
fig, ax = plt.subplots(1, 2, figsize=(12, 6))
ax[0].imshow(image, cmap='gray')
ax[0].set_title('Blurred Input')
ax[1].imshow(deconvolved, cmap='gray')
ax[1].set_title('Deconvolved Result')
plt.show()
ACTF{DeEptCUdAR1VQUZ}
unstoppable
Explore my previous post for detailed analysis.